[백준/1238/파이썬] 파티

https://www.acmicpc.net/problem/1238

1238번: 파티

Problem

• N개의 숫자로 구분된 각각의 마을에 한 명의 학생이 살고 있다. 어느 날 이 N명의 학생이 X (1 ≤ X ≤ N)번 마을에 모여서 파티를 벌이기로 했다
• 각각의 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다. 하지만 이 학생들은 워낙 게을러서 최단 시간에 오고 가기를 원한다.
• 이 도로들은 단방향이기 때문에 아마 그들이 오고 가는 길이 다를지도 모른다. N명의 학생들 중 오고 가는데 가장 많은 시간을 소비하는 학생은 누구일지 구하여라.

조건

• 이 마을 사이에는 총 M개의 단방향 도로들이 있고 i번째 길을 지나는데 Ti(1 ≤ Ti ≤ 100)의 시간을 소비한다.
• 첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다.
• 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어온다. 시작점과 끝점이 같은 도로는 없으며, 시작점과 한 도시 A에서 다른 도시 B로 가는 도로의 개수는 최대 1개이다.
• 모든 학생들은 집에서 X에 갈수 있고, X에서 집으로 돌아올 수 있는 데이터만 입력으로 주어진다.

SOL

각자 학생의 집에서, X 까지 방문을 했다가, 또 X에서 최단거리로 각자의 집으로 돌아와야하는 문제이다.

 

Dijkstra를 이용하여, 출발노드 - target, target - 출발노드 거리 계산하기

 

Dijkstra를 사용해서, 출발노드에서 target노드까지 최단거리로 간다음, target노드에서 최단거리로 출발노드로 오는 거리를 매번 계산해서 갱신시키는 방법을 떠올렸고, 구현을 했음!

 

#파티
#다익스트라
import sys
import heapq
input= sys.stdin.readline
INF=int(1e9)
N,M,X=map(int,input().split())
graph=[[] for _ in range(N+1)]

for _ in range(M):
    a,b,cost=map(int,input().split())
    graph[a].append((b,cost))

def Dijkstra(start,end):
    hq=[]
    dist=[INF for _ in range(N+1)]
    heapq.heappush(hq,(0,start))
    dist[start] = 0
    while hq:
        distance,now=heapq.heappop(hq)
        if dist[now] < distance:
            continue
        for nxt in graph[now]:
            cost=distance+nxt[1]
            if cost<dist[nxt[0]]:
                dist[nxt[0]]=cost
                heapq.heappush(hq,(cost,nxt[0]))
    return dist[end]

ans=-1
#start는 모든 node
for i in range(1,N+1):
    d= Dijkstra(i,X) + Dijkstra(X,i)
    ans=max(ans,d)

print(ans)

 

2. X를 기준으로, 그래프 자체를 뒤집어서 생각해주기. ( 좀 더 실행시간이 빠른 풀이)

 

X를 기준으로,  정방향 그래프, 역방향 그래프를 설정해준뒤, 각각 X에 대해서 Dijkstra를 실행해주고, distance를 계산해주면 된다. 이 풀이가 성립하는 이유는 그림으로 보면 확 와닿는다.

 

우리가 직관적으로 생각을 한다면, 문제에서 제시해준대로 , A->B->A로 생각을 해줄 수 있다. 

하지만, 우리는 Target 노드가 명확하다. 즉, 우리는 결국 "X"에 도착하는것이 목적이다.

그렇다면, "X"에서 시작해서, 모든 노드로 가는 길 == 돌아오는 길이 성립하게 된다.

아래의 그림에서 보자면,  A->B->A 에서, B->A (주황색 길)이 돌아오는 길이 되는거다.

 

그렇다면, A->B까지의 길도 "B"의 입장에서 나타낼 수 있을까? 직관적이진 않지만, 가능하다.

A->B,B->A 코스트가 다르기 때문에, A->B 로 가는 Cost를 B->A로 가는 코스트로 저장하는 또 다른 그래프를 설정해주면 된다. 그러면, A->B 로가는 길을 "B"의 입장에서 나타낼 수 있게 된다. 이 그래프가 바로, A->B의 역방향 그래프이다.

A->B가 원래 cost 4로 연결되어 있는데, B->A가 4로 연결되어있는걸 볼 수 있다. 따라서, A->B로 가는게 우리의 논리적인 의미 이지만, 실제로 그래프에서는 B->A로 가는걸로 처리해야하기 때문에, 아래와 같은 그래프 정보가 필요하고, 실제로 이렇게 함으로써, 실행시간이 상당히 단축되는 효과가 발생한다!

 

 

 

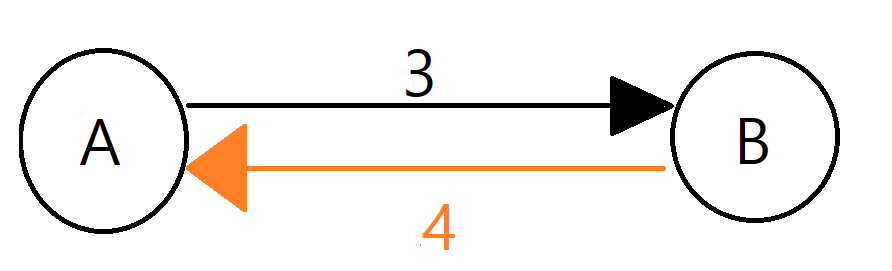
# 파티
# 그래프 2개
import sys
import heapq
input= sys.stdin.readline
INF=int(1e9)
N,M,X = map(int,input().split())
graph_1=[[] for _ in range(N+1)]
graph_2=[[] for _ in range(N+1)]

for i in range(M):
    a,b,cost=map(int,input().split())
    graph_1[a].append((b,cost))
    #graph_2에는 역방향을 저장해준다
    graph_2[b].append((a,cost))

def Dijkstra(hq,dist,graph):
    while hq:
        distance,now=heapq.heappop(hq)
        if dist[now]<distance:
            continue
        for nxt in graph[now]:
            cost=distance+nxt[1]
            if cost<dist[nxt[0]]:
                dist[nxt[0]]=cost
                heapq.heappush(hq,(cost,nxt[0]))

dist_1=[INF for _ in range(N+1)]
dist_1[X] =0
hq_1=[[0,X]]
Dijkstra(hq_1,dist_1,graph_1)

dist_2=[INF for _ in range(N+1)]
dist_2[X] =0
hq_2=[[0,X]]
Dijkstra(hq_2,dist_2,graph_2)

ans=-1
for i in range(1,N+1):
    ans=max(ans,dist_1[i]+dist_2[i])

print(ans)