https://www.acmicpc.net/problem/1720
1720번: 타일 코드
2×N 크기의 넓은 판을 1×2 (또는 2×1) 크기와 2×2 크기의 타일로 채우려고 한다. 여러 가지 경우가 있을 수 있으므로, 각각을 하나의 코드로 대응시켜서 암호화에 이용하려고 한다. 그런데 문제가
www.acmicpc.net
Problem
- N이 주어지면, 전체 타일 코드의 개수를 구하는 프로그램을 작성하시오.
조건
- 서로 좌우 대칭을 이루는 중복된 표현은 한 가지 경우로만 처리한다.
- 첫째 줄에 타일의 크기 N(1 ≤ N ≤ 30)이 주어진다.
SOL
"좌우 대칭을 이루는 중복된 표현"을 이해하기가 참 어려웠던 문제이다.
좌우대칭이라고 하면, 일반적으로 반을 딱 나눴을 때, 좌,우가 같으면 다 좌우대칭이라고 생각한다.
하지만, 이 문제에서 좌우대칭을 이루는 중복된 표현은 , 아래와 같은 타일을 1가지 경우로만 처리한다는거임.
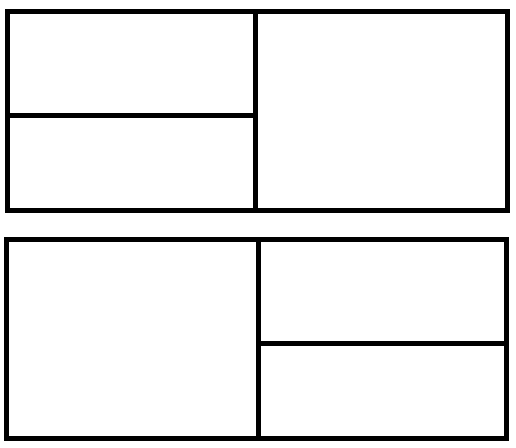
이 문항을 처음부터, 이해했다고하면, 이해력이 정말 좋으신 분이다. (저는 여기까지 이해하는것도 어려웠습니다)
우리는 문제를 풀기위해서 2가지 방법을 생각할 수 있다.
- 전체 경우에서 "좌우 대칭을 이루는 중복된 표현"을 걸러주기.
- "좌우 대칭을 이루는 중복된 표현"을 하나하나 세어주면서, 규칙성을 찾기
전체 경우에서 "좌우 대칭을 이루는 중복된 표현"을 걸러주기

모든 경우의 수 : F(N) = F(N-1) + 2*F(N-2)
단순히 모양이 같으면, 똑같은걸로 생각하고, F(N)/2이 정답이라고 생각할 수 있다. 하지만, 몇가지 반례가 생기게 된다.
예를들어
1번 같은 경우는, 문제의 조건에 맞는 경우이다.(2개가 존재하면, 1개로 줄여야함)
2번 같은 경우는, 문제의 조건에 맞지 않은 경우이다. (이 경우는 이미 1개의 경우이다)
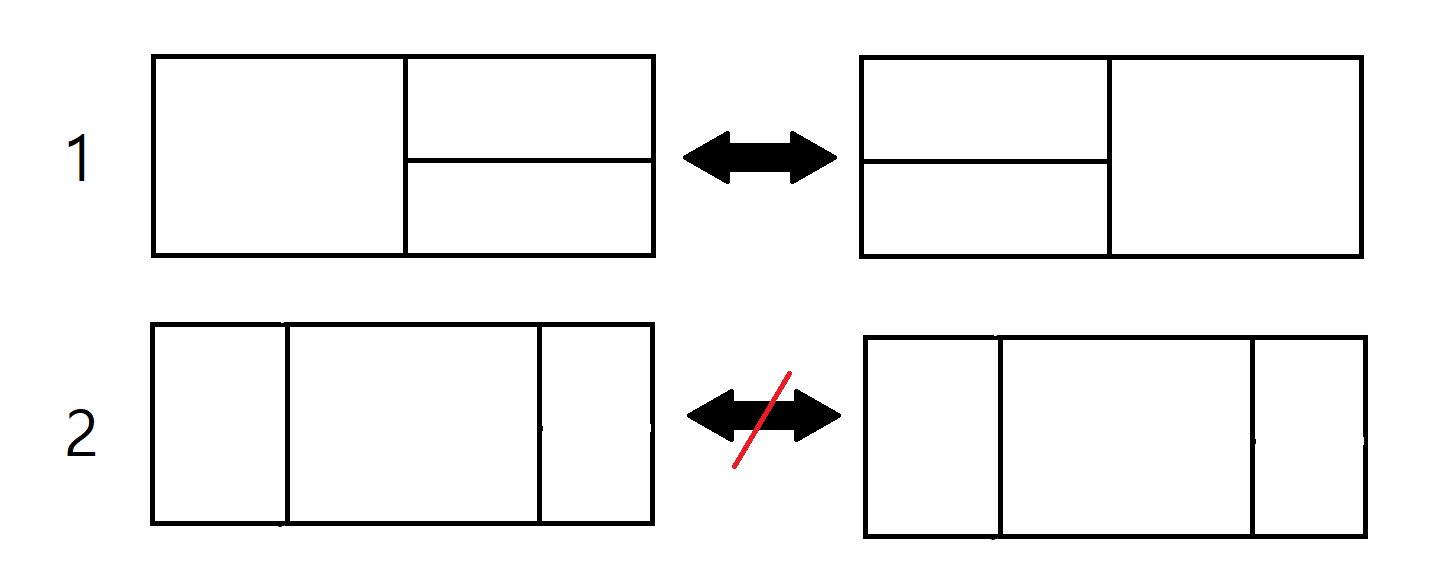
따라서, 2번 같은 경우도 모두 1/2을 해주게 되면, 우리가 구하는 정답이 아니게 된다.
그렇다면, 2번 같은 경우들을 다 구해주거나, 1번 같은 경우를 그냥 다 새롭게 세어줘서 규칙성을 발견해야하는데,
2번 같은 경우가 뭐가 있을까 생각을 먼저 해보자.
※ 다른 블로그들을 보면, 2번 같은 경우를 보통 "자기자체로 좌우대칭인 친구"들이라고 하는데, 글로 보면, 가독성을 해친다고 생각해서, 나는 Case 2라고 하겠다. 의미적으로 자기자체로 좌우대칭인 친구가 맞다.
Case2
- (전체경우 - Case2)/2 + Case2를 해주면, 전체경우, Case2만 문제를 해결할 수 있다.
- Case 2의 경우를 어떻게 구할까?
- Case 2를 생각해보면, Case2는 Case2에 해당하는 타일을 반을 쪼개서, 둘을 바꿨을때, 구성하는 패턴까지 똑같아서, 둘을 바꿔도 똑같은 경우라고 생각할 수 있다. 따라서, 자기 자체로 좌우대칭인 경우를 구해주면 된다.
- 이러한 경우를 생각해주면, 4가지가 있다.
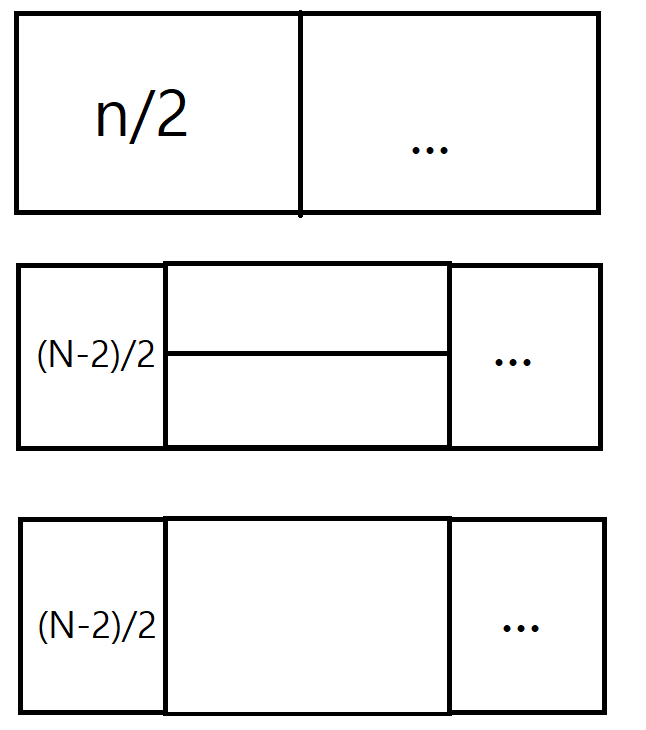

Case 2
(전체경우 - Case2)/2 + Case2
- N이 짝수 : F(N/2) + 2*F((N-2)/2) , (DP[n] - (2*DP[(n-2)/2] + DP[n/2]))/2 + (2*DP[(n-2)/2] + DP[n/2]))
- N이 홀수 : F(N-1)/2 , (DP[n] - DP[(n-1)/2])/2 + DP[(n-1)/2])
# 타일문제의 끝판왕
# 정말 어렵다.
# DP
N = int(input())
DP = [0]*31
DP[1]=1
DP[2]=3
for i in range(3,N+1):
DP[i] = DP[i-1] + 2*DP[i-2]
if N>=3:
if N%2==0:
print((DP[N] - (2*DP[(N-2)//2] + DP[N//2]))//2 + (2*DP[(N-2)//2] + DP[N//2]))
else:
print((DP[N] - DP[(N-1)//2])//2 + DP[(N-1)//2])
else:
print(DP[N])
'알고리즘 문제(SOL)' 카테고리의 다른 글
| [백준/5557/파이썬] 1학년 (0) | 2022.01.19 |
|---|---|
| [백준/1495/파이썬] 기타리스트 (0) | 2022.01.18 |
| [백준/1309/파이썬] 동물원 (0) | 2022.01.18 |
| [백준/2240/파이썬] 자두나무 (0) | 2022.01.17 |
| [백준/11066/파이썬] 파일 합치기 (0) | 2022.01.17 |