https://www.acmicpc.net/problem/3101
3101번: 토끼의 이동
첫째 줄에 N, K가 주어진다. (1 ≤ N ≤ 100,000, 1 ≤ K ≤ 300,000) N은 행렬의 크기, K는 토끼가 점프한 횟수이다. 둘째 줄에는 'U','D','L','R'로 이루어진 문자열이 주어진다. 이 문자열의 길이는 K이며, 토
www.acmicpc.net
Problem
- 토끼는 지금 1이 있는 칸에 있다. 토끼는 인접한 칸으로 점프할 수 있다. (위, 아래, 오른쪽, 왼쪽)
- 토끼가 점프한 방법이 주어졌을 때, 토끼가 방문한 칸에 있는 수의 합을 구하는 프로그램을 작성하시오. 같은 칸을 여러 번 방문할 경우에도, 방문할 때 마다 더해야 한다. 토끼가 행렬을 벗어나는 경우는 없다.
조건
- 1부터 N2까지 수가 지그재그 대각선 순서로 N*N 행렬에 채워져 있다.
SOL
간단해 보여도 절대 간단하지 않은 문제였다.. 솔직히 지그재그로 배열을 채우는 연습은 한번도 안해봤는데,
진짜 어려운거 같다. 그리고 이 문제는 O(N)으로 지그재그로 반복을 돌아야한다.
나중에 Codeup에 기초배열 부분을 다 푸는것도 블로그에 올려야겠다.
1. 지그재그로 배열을 채운다.
아는값: Grid(좌표)값
우선, N=4일때, 지그재그로 채워보자.

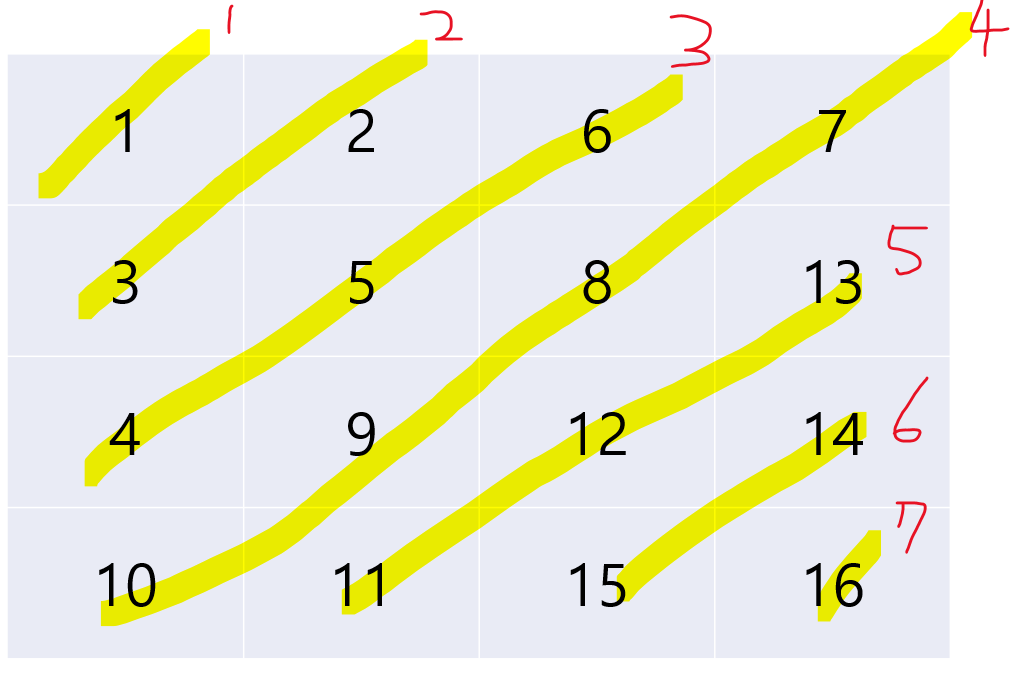
위와 같은 규칙으로 배열이 채워질거다. 그리고, 이렇게 채울때 특징이 1개가 있는데, 제일 큰 대각선(4번 대각선)을 기준으로 원소의 갯수가 늘어났다가 줄어드는걸 볼 수 있다.
- 우리는 이 대각선을 기준으로 생각을 해줄거다.
- 1~N대각선 까지는 원소의 갯수가 늘어나고, N+1~2*N-1까지는 원소가 줄어든다.
- 그래서, 우리는 각 대각선의 시작점을 구하는 함수를 구현할거임!
- 이 시작점들을 1차원 배열에 mapping 해줄거다. mapping 해주기위해서, 규칙을 찾아보자.
- 1~N대각선 까지
- 시작점 = 그 이전의 시작점 + idx
- N+1~ 2N-1 까지
- 시작점 = 그 이전 시작점 + N - (idx%N)
#각 지그재그의 시작점을 담는 배열
firstNumbers=[0]*(N*2)
firstNumbers[1] =1
# 지그재그의 시작점을 계산하는 방법
def getLength(idx):
if idx<=N:
return idx
return N -idx%N
#if N=4, [0,1,2,4,7,11,14,16]
for i in range(2,N*2):
firstNumbers[i] = firstNumbers[i-1] + getLength(i-1)
2. 토끼를 움직여준다.
토끼를 움직여 줄때, 우리는 시작점에서 얼마나 더 가는지만 알면, matrix의 값을 알 수있다.
그래서, 각각의 시작점에서 해당 좌표까지 갈때의 관계를 알아야한다.
이 부분은 찾기가 상당히 힘든 부분이고, 어떻게 구현하느냐에 따라서, 달라질 수 있고, 난 N=4,5를 예시로 들면서 진짜 이렇게 되는지 체크하면서 해봤다.
일단, 대각선이 짝수냐,홀수냐에 따라서 진행방향이 뒤바뀐다. 그래서, 더해주는 값도 바꿔야한다.
좌표가 있는 대각선 (기울기) : x+y-1
- 좌표가 있는 대각선 <=N인 경우
- 좌표가 있는 대각선이 짝수인 경우
- 진행할수록, row(행)의 값은 증가하고, C(열)의 값은 감소하는 형태를 띈다. 만약, N=4, 좌표가 (2,3)이면, 좌표가 있는 대각선은 (2+3) -1 , 4번째 대각선이다. (1,4) : 7, (2,3):8, (3,2): 9 이므로, 1*r-1만큼 증가. 즉, matrix의 값: 첫시작점 + (r-1)
- 좌표가 있는 대각선이 홀수인 경우
- 진행할수록, row(행)의 값은 감소하고, C(열)의 값은 증가하는 형태를 띈다. 만약, N=3, 좌표가 (2,2)이면, 좌표가 있는 대각선은 (2+2) -1 , 3번째 대각선이다. (3,1) : 4, (2,2):5, (1,3): 6 이므로, 1*c-1만큼 증가. 즉, matrix의 값: 첫 시작점 + c-1
- 좌표가 있는 대각선이 짝수인 경우
- 좌표가 있는 대각선 >N인 경우
- 좌표가 있는 대각선이 짝수인 경우
- 진행 할수록, 행은 증가, 열은 증가한다. 예를들어, N=4일때, (3,4) ->(4,3)으로의 진행을 보자. 1이 N-c개만큼 쌓인다. matrix의 값: 첫 시작점 + N-c
- 좌표가 있는 대각선이 홀수인 경우
- matrix의 값 : 시작점 + (N-r)이 된다.
- 좌표가 있는 대각선이 짝수인 경우
# 토끼 깡총깡총
# 지그재그로 배열을 채우는 방법?
import sys
input= sys.stdin.readline
N,K = map(int,input().split())
#현재 위치
R,C = 1,1
#각 지그재그의 시작점을 담는 배열
firstNumbers=[0]*(N*2)
firstNumbers[1] =1
# 지그재그의 시작점을 계산하는 방법
def getLength(idx):
if idx<=N:
return idx
return N -idx%N
for i in range(2,N*2):
firstNumbers[i] = firstNumbers[i-1] + getLength(i-1)
def moving(r,c):
#몇번째 대각선인지 알아내기
lineNumber = r+c-1
#lineNumber째 대각선 시작점
firstNumber = firstNumbers[lineNumber]
# 1~N번째 대각선
if lineNumber<=N:
if lineNumber %2==0:
return firstNumber+(r-1)
else:
return firstNumber+ (c-1)
#N+1~ 2*N-1번째 대각선까지.
else:
if lineNumber%2==0:
return firstNumber+(N-c)
else:
return firstNumber+(N-r)
ans=1
for m in list(input().rstrip()):
if m =="U":
R-=1
elif m=="D":
R+=1
elif m=="L":
C-=1
elif m=="R":
C+=1
ans +=moving(R,C)
print(ans)'알고리즘 문제(SOL)' 카테고리의 다른 글
| [백준/17472/파이썬] 다리 만들기 2 (0) | 2022.01.31 |
|---|---|
| [백준/1015/파이썬] 수열 정렬 (0) | 2022.01.31 |
| [백준/16236/파이썬] 아기 상어 (0) | 2022.01.30 |
| [백준/1256/파이썬] 사전 (0) | 2022.01.29 |
| [백준/17141/파이썬] 연구소 2 (0) | 2022.01.29 |