그래프를 배우게 되면, 제일 처음 배우게되는 일종의 정립되고, 문제에서 아주 자주나오는 스테디셀러인 친구들이 있다.
DFS , BFS가 뭔지 살펴보기 전에, DFS,BFS는 완전탐색알고리즘이고, 가능한 수를 전부 다 뒤지는 알고리즘의 일종이다.그래서, 느리지만, 정답을 무적권 찾을수 있다는 기본적인 특성이 있기 때문에, 이건 알고가자.
오목을 한다고 생각해보자!
여러분은 백돌이고, 여러분의 차례이다. 그럼 , 어디를 막을 수 있을까? 생각을 하게 될것이다.



여러분은, 위와 깉이 다양한 경우의 수를 생각하면서, 오목을 할 것이다. 그럼 , 이때, 여러분의 생각의 방식에 따라서, 2가지로 나눌 수 있다.
첫번째. 1가지의 경우에 대해서 생각한 뒤, 그 경우일 때, 일어나는 경우를 계속 생각하는 방법 .
오목으로 생각하면, 내가 놓고, 상대방이 놓고, 그 뒤 상황을 생각하는 방법.
그림으로 보면 , 1 -> 2->3->4 이런식으로 차례대로 생각하는 방법

두번째, 1번째 경우의 수를 다 따지고 , 1번째에 대한 경우의 수에 대한 각각의 경우의 수를 다 따지고,
"1->2->3->4->5->6->7->8->9" 순으로생각하는 방법.
말이 어렵게 느껴지면, => 매 단계에서 가능한 모든 경우의 수를 확인한다.

이렇게 두가지 생각방법이 있을거다. 뭐가 DFS,BFS일까?
DFS(Depth Fisrt Search)
DFS
- 한 경우에 대한, 경우를 끝까지 다 생각하는 방법.
- 한 우물만 판다라고 표현하기도 한다.
- Stack, 재귀함수를 통해 구현한다.
- 방문했던 Node , 이미생각했던 판은 더 이상 생각하지 않는다.

자, 이제 DFS의 느낌이 뭔지 정리가 됬다.
우리는 , 그래프를 다루는거니까, 그래프로 생각해보자! DFS 탐색을 한다면 ??
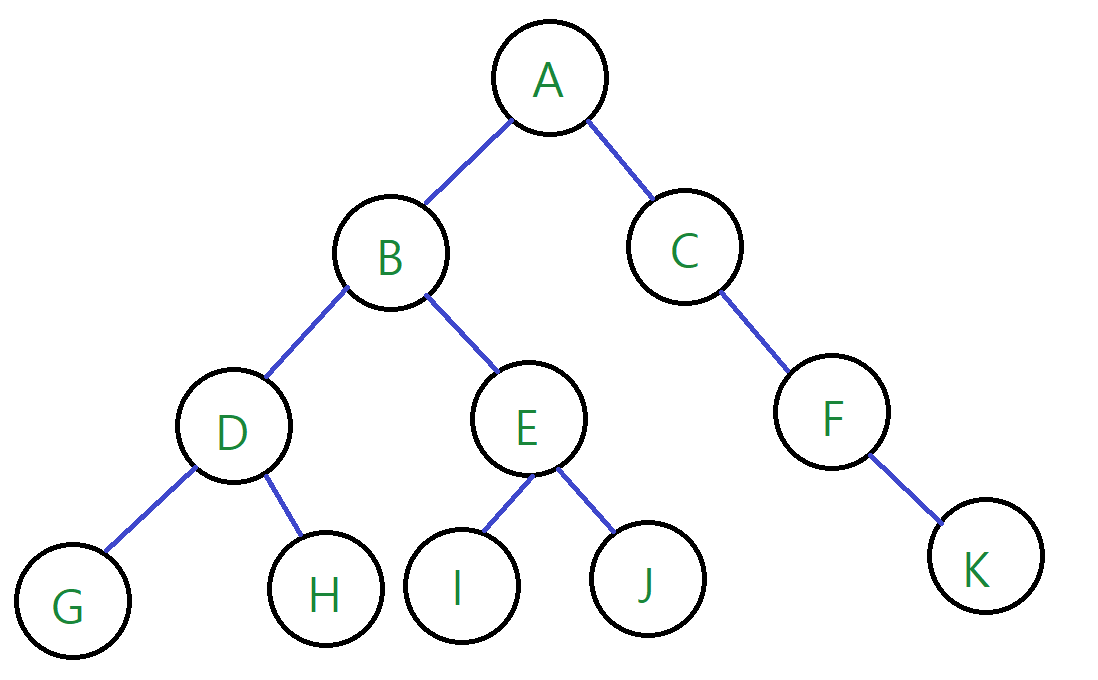
순서 : A ->B -> D-> G -> H ->E -> I -> J ->C->F->K
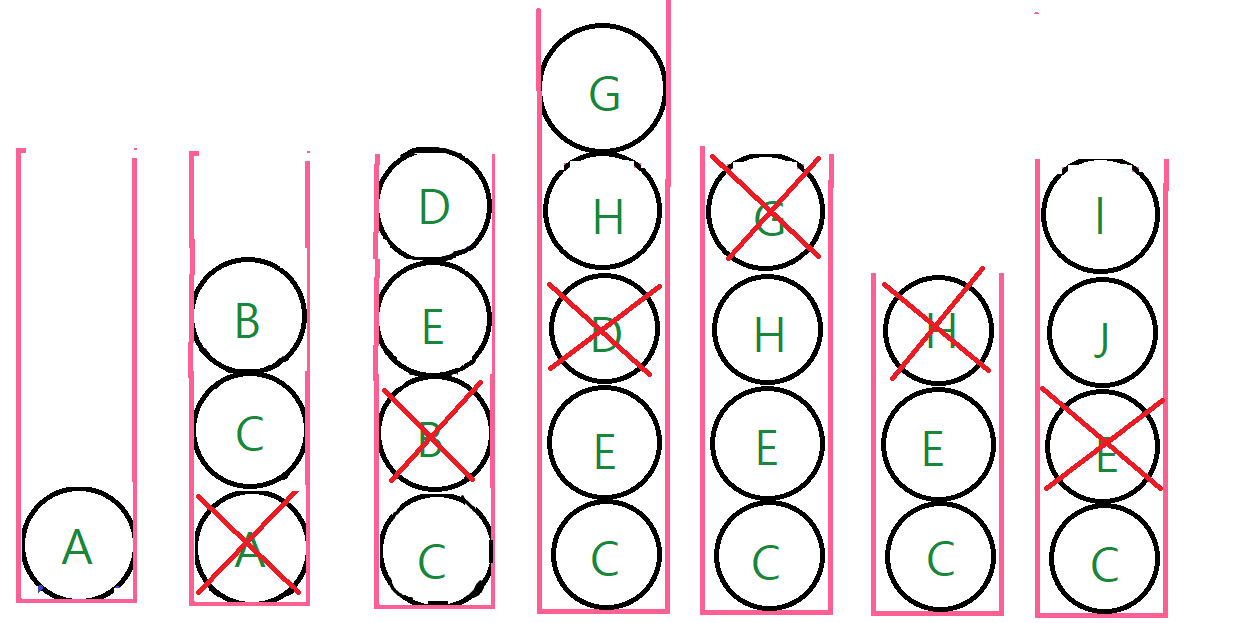
이 순서가 어떻게 나오는지 , 스택까지 보면서 확인해보자. DFS에서는 스택/재귀함수를 이용한다고 했으니까.
DFS 한 단계에서 POP과 append 두 가지 일을 동시에 처리합니다.
- POP: 스택 TOP의 노드를 꺼냅니다.
- append: POP한 노드를 지우면서, 그 노드의 자식(인접한) 노드를 모두 스택에 넣습니다. 자식이 존재하지 않는다면, pop을 합니다.
코드로 구현하면 ?
import sys
sys.setrecursionlimit(10000)
N,M = map(int,input().split())
adj = [[] for _ in range(N)]
v_check = [False for _ in range(n + 1)]
# 인접 리스트로 구현
for _ in range(M):
y,x = map(int,input().split())
adj[y].append(x)
adj[x].append(y)
# 인접 행렬로 구현한다면?
# adj = [[]*N for _ in range(N)]
***for _ in range(M):
y,x=map(int,input().split())
adj[y][x] =1
adj[x][y] =1***
#재귀함수 이용
def dfs(n):
v_check[n] = True
#print(x, end = ' ')
for i in edge[n]:
if not d_check[i]:
dfs(i)스택으로 구현한다면?
# Pseudo Code
def DFS(st_node):
stack = [st_node, ]
while True:
if not stack:
print('Stack is Empty')
return None
TOP = stack.pop()
if TOP == Target:
return TOP
stk.append(children)
# children을 stack에 쌓기
# Target을 찾거나, stack이 빌 때까지 while문 반복
글이 길어져서 , 다음편으로 넘겨야 겠다. Next : BFS(Breadth First Search)
'알고리즘 개념(Concept)' 카테고리의 다른 글
| [알고리즘,개념] Backtracking (0) | 2022.01.05 |
|---|---|
| [알고리즘,개념,활용] 길을 찾자! (0) | 2021.11.18 |
| [개념/파이썬/알고리즘] BFS(Breadth First Search) (0) | 2021.11.13 |
| [개념,그래프] 인접행렬 ,인접리스트 - 그래프를 코드로 ! (0) | 2021.11.11 |
| [자료구조,개념] 그래프, 트리 (graph,tree) (0) | 2021.11.11 |