https://www.acmicpc.net/problem/11085
11085번: 군사 이동
전쟁 당시 Baekjoon World의 국왕은 Cube World를 공격할 작전을 세운 적이 있습니다. Baekjoon World와 Cube World는 p개의 지점과 w개의 길로 표현됩니다. 모든 길은 양방향이며, 각 길마다 너비가 존재하여
www.acmicpc.net
Problem
- 전쟁 당시 Baekjoon World의 국왕은 Cube World를 공격할 작전을 세운 적이 있습니다. Baekjoon World와 Cube World는 p개의 지점과 w개의 길로 표현됩니다. 모든 길은 양방향이며, 각 길마다 너비가 존재하여 이에 비례하는 수의 군사가 지나갈 수 있습니다.
- 그런데 전쟁 때문에 어느 길로 보냈는지에 대한 기록이 불타 없어져 버렸습니다. 전쟁사를 완성하려면 이 기록이 꼭 필요합니다. 위대한 과학자인 당신이 다시 복구해 주세요.
조건
- Baekjoon World의 국왕은 군사들이 뭉치는 것이 유리하다고 생각해서, 미리 Cube World로 가는 경로를 정해 두고 그 경로로만 모든 군사를 보냈습니다. Baekjoon World의 국왕은 총명해서, 경로 상에 있는 길 중 너비가 가장 좁은 길의 너비를 최대화하는 경로를 택했습니다.
- 첫 줄에 p와 w가 공백을 사이에 두고 주어집니다. (2 ≤ p ≤ 1 000; 1 ≤ w ≤ 50 000)다음 w줄에 길이 연결하는 두 지점 wstart, wend,와 길의 너비 wwidth가 공백을 사이에 두고 주어집니다. (0 ≤ wstart, wend < p; wstart ≠ wend; 1 ≤ wwidth ≤ 1 000)
- 다음 줄에 Baekjoon World의 수도 c와 Cube World의 수도 v가 공백을 사이에 두고 주어집니다. (0 ≤ c, v < p; c ≠ v)
SOL
처음에는 , 3- 5 로 가는 경로 중, 최단 거리만 찾으면 되는 줄알고, 다익스트라를 이용하거나, BFS를 이용해서 찾으면 될줄 알았는데, 16이라서 띠용 했다.그리고 MST인가 생각을 했지만, 모든 노드를 방문하는 경우 중에 최소를 찾는게 아니므로, MST는 아닐거라고 생각했다. 문제를 다시 읽어보니, "경로 상에 있는 길 중, 너비가 가장 좁은 길의 너비를 최대화 했다"
이게 , 인간이라면 이런 최대 중에 최소, 최소 중에 최대 , 1개가 유일하다고 생각하는 값에 2차원적인 개념이 안와닿는다.(신기하게도)
예를들어, 1,2,3,4,5 중에 최소을 찾으라고 하면, 5를 쉽게 찾을 수 있다. 하지만, 사실 이 1,2,3,4,5가 어떤 수열에서의 최댓값 들을 모아놓은 것이라면, 최댓값 중에 최솟값은 "1"이 되어버릴거다.
그러니까, 3 -5로가는 경로들 중, 가장 좁은 길의 넓이가 최대가 되는 경로를 찾는 문제이다.
해당 문제의 예제를 그래프 관계로 나타낸다면, 아래와 같게 된다.
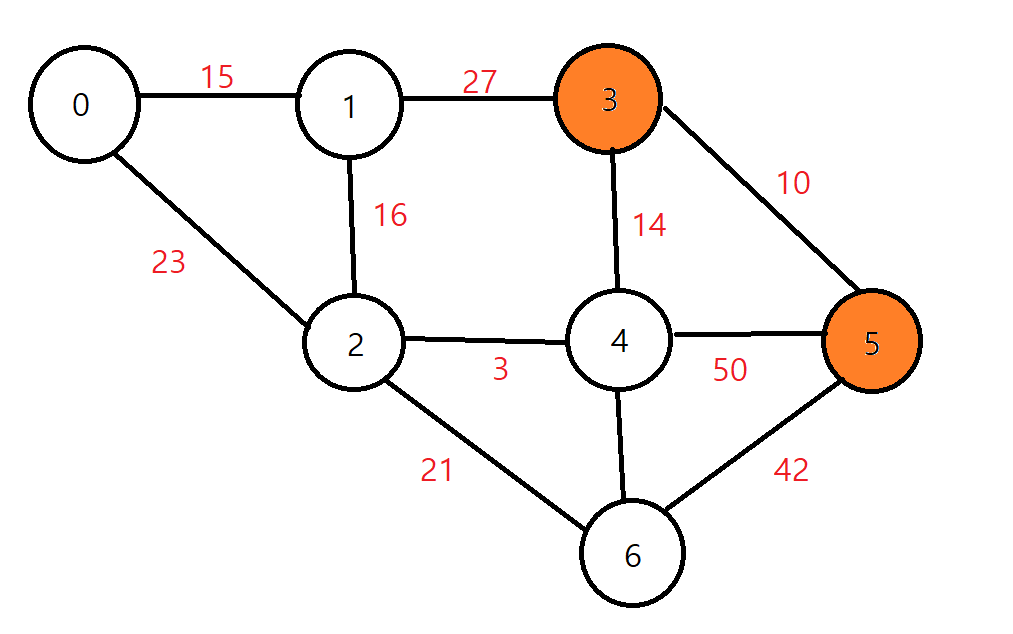
이때, 3 ->5로 가는 경로는 엄 ~청 많다.
3 ->5 ,3->4->5,3->4->6->5 등등
이 많은 경로 중에서, 이 경로값들 중 최솟값만 모아놓는다고 생각했을 때, 그 중에 최대값을 구하는 문제이다.
좀 더 쉽게 생각하면, 최대값을 가지는 경로 중에, 최소의 가중치를 갖는 edge를 찾는 문제라고 생각할 수 있다.
완전탐색
예를들어, 3->5는 10 , 3->4->5 는 14, 3->4->6->5 는 14,3->4->2->6->5 는 2가 각각 해당 경로에서의 최솟값일 거고, 3->5로 가는 경로를 모두 모아봤을 때, 각각의 경로에서 최솟값들도 모이겠죠? 그 중에서 최댓값을 찾는 문제이다.
하지만, 노드가 1000개이고, 간선의 관계는 5만개가 나올 수 있다. 3 ->5로 가는 모든 경로를 탐색하려면 BFS/DFS를 생각해줘야하는데, 보통 BFS/DFS는 O(V^2)이라고 알려져 있다. 하지만, 각각의 탐색경로에 가중치가 들어가므로, BFS/DFS에서 조건이 들어가게 될거고, DFS로 한다면 , backtracking을 해야할거다. 왜냐하면, 1->2->4->5 와 1->3->5는 다른 경우이기 때문에, 단순히 정점의 갯수의 ^2만큼 방문하면되나?
아니다. 0 ->1->3->5 와 0->1->2->4->5는 엄연히 다른경우이므로, 재귀적으로 구현할 수 밖에 없을거고, 가중치를 그때마다 생각해준다면 한 노드에 연결되어있는 간선의 갯수만큼 곱해지는 관계가 될것이다.
간선의 갯수가 최대 50,000인데, 한 노드에 10개씩 연결되어있는 노드가 10개만 있어도, 10^10, TL이 발생한다.
Union - Find 구조
사실, MST인줄 알고, Union -Find 구조를 적용시키려다가, 생각이 들었고, 블로그들을 보면서 정리된 방법이다.
두 노드를 Union해준다. Union이 되었다는 의미는, 이제 서로를 통해서, 서로에게 도달할 수 있다는 의미이다.
예를들어, 3,4,5가 union 되었으면, 3->5,4->5,5->4로 갈 수 있는 방법이 마련되었다는 의미이다.
이때, 연결을 해줄 때, 가중치가 큰 순서대로 연결을 해준다.
가중치가 큰 순서대로 연결을 해줄 때, 우리가 생각해야 하는 부분은 최초로 3-5가 연결되는 지점이다.
가중치가 큰 순서대로 연결하는 과정에서, 최초로 3-5가 연결되는 지점이라는 건, 3 -5가 연결되는 최솟값들 중에서 최댓값을 가지는 순간이라고 생각할 수 있다.
왜냐하면, 3 - 5가 서로 같은 부모 노드를 갖고 난 이후에, 남은 거리값들은 (큰 순서대로 연결되었기 때문에) 당연히 최초의 값들보다 작아질 수 밖에 없고, 3 -5로 통하는 경로의 값이 된다. 그래서, 최솟값들 중에 최대값이라고 볼 수 있고, 3 -5로 통하는 모든 경로들 중의 최솟값 중 최댓값이라고 생각할 수 있다.
그렇다면, 최댓값 순서대로 dist를 정리해놓고 순서대로 뽑아야하는데, 좋은 자료구조가 있을까? Heapq(우선순위 큐)를 이용하면 된다!
역시, 효율적인 알고리즘은 직관적이지 않다.. :(
#군사이동
#MST 인듯하면서, 아닌 문제!
import sys
import heapq
input= sys.stdin.readline
P,W = map(int,input().split())
C,V = map(int,input().split())
edges=[]
def find(target):
if target==parent[target]:
return target
parent[target] = find(parent[target])
return parent[target]
def union(a,b):
a=find(a)
b=find(b)
if a !=b:
parent[a] =b
parent=[x for x in range(P+1)]
ans=0
for i in range(W):
ws,we,dist=map(int,input().split())
heapq.heappush(edges,(-dist,ws,we))
while edges:
cost,start,end=heapq.heappop(edges)
cost = -cost
union(start,end)
if find(C) ==find(V):
ans=cost
break
print(ans)'알고리즘 문제(SOL)' 카테고리의 다른 글
| [백준/16933/파이썬] 벽 부수고 이동하기3 (0) | 2022.02.13 |
|---|---|
| [백준/17142/파이썬] 연구소 3 (0) | 2022.02.12 |
| [백준/2442/파이썬] 별 찍기 -5 (0) | 2022.02.11 |
| [백준/1920/파이썬] 수 찾기 (0) | 2022.02.11 |
| [백준/16922/파이썬] 로마 숫자 만들기 (0) | 2022.02.10 |