https://www.acmicpc.net/problem/11660
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
Problem
- N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
조건
- 첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다.
- 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
SOL
특정 구간의 합 (누적합)을 구하는 방법은 많다. 여러가지 방법에 대해서 생각해보자.
완전탐색
직관적이고, 가장 쉽게 떠오르는 방법은 , 이중 반복문을 실행시켜주는 것이다.
아무런 제약없이 , (x1,y1) ~ (x2,y2)구간의 누적합을 구하라고 한다면, 아래와 같이 구현할 것이다.
.....
for i in range(x1,x2):
for j in range(y1,y2):
total += board[i][j]
....하지만, 위의 풀이는 특정 구간이 정해질 때마다, 2중 반복문을 돌아야하므로, 위의 문제에서는 시간제한안에 풀지 못한다. O(M*N^2)이므로, 불가능하다.
누적합 이용하기
1차원 배열에서 , 누적합을 이용해서 구간합을 쉽게 구하는 방법은 잘 알려져있다.
예를 들어, A= [ 1,2,3,4,5 ] 라고 한다면, 누적합 S =[ 1,3,6,10,15] 를 구해주고, (x1,x2)까지의 구간합을 구해주라고 한다면, S[x2] - S[x1-1]을 해주면 된다. (2,4) 까지 구간합을 구한다고 하면, S[4] - S[1]을 해주면 된다.
2차원 배열에서도 위처럼, 누적합을 이용할 수 없을까 ?
아래와 같이 A = [[1,2,3],[4,5,6],[7,8,9]]가 있다고 하자. 우선, (1,1) ~ (2,2) 까지 누적합을 어떻게 구할 수 있을까?


사람이 구한다면, 1+2+4+5 , 12로 쉽게 구할 수 있을거다. 1차원 누적합을 구하듯이, 일단, 1차원 누적합을 구해주고,
그 다음, 열끼리 합쳐주면, 누적합이 완성된다! 하지만, 이건 시작점이 (0,0)에서 고정되어 있는 형태로 구해진 상태이다.

즉, (0,0 ~ N-1,N-1)의 누적합을 구했지만, 우리가 원하는건 특정 구간의 합을 구하는 과정이다.
먼저, 행의 누적합을 구하고, 열의 누적합을 구해주면, (0,0~ x1,y1)까지의 누적합은 쉽게 구해진다.
- "이 누적합의 표를 가지고, 쉽게 누적합을 구할 수 있지 않을까" 아주 심플하면서 강력한 아이디어이다.
이 표를 이용해서 , (2,2) ~ (3,3) 까지의 누적합을 구한다고 생각해보자.


우선, (2,2) ~ (3,3)의 누적합은 5+6+8+9 = 28 이다. 우리가 아는 정보는 (0,0) ~ (a,b,) 까지의 누적합이다.
그렇다면, (3,3)의 누적합에서, 어떤 정보를 빼면 되지않을까 ? 어느 부분을 빼면 될까?
이 부분을 보고 싶다면, 누적합의 부분을 쭉 나열해보면, 수식적 (수학적)으로 보이기 시작한다.
- 필요한 정보 : (2,2) ~ (3,3) , A[2][2]+ A[2][3] + A[3][2] + A[3][3]
- 우리가 아는 정보 : (1,1) ~ (3,3) => A[1][1] + A[1][2] .... + A[3][3]
- 제외할 정보 : A[1][1] +A[1][2] +A[1][3] +A[2][1]+A[3][1] , 수식적으로 보면, 이렇게 되지만, 우리가 아는 정보를 더 이용해보자!
주황색 부분은, (1,1) ~ (1,3) 의 누적합으로 나타낼 수 있다. (1,1) ~ (1,3) = A[1][1] +A[1][2] +A[1][3]
어, 그럼, 빨간색 부분은 , A[1][1]만 있으면, (1,1) ~ (3,1) 까지의 누적합이다. A[1][1] +A[2][1]+A[3][1]
그럼, 우리는 누적합을 다 아니까, A[1][1] 까짓거 한번 더 계산해주고, 중복되는 부분 더 해주면 되는거 아니야? 라는 당연한 생각을 해주면 된다.
이렇게 되면, 우리는 누적합의 표만 가지고, 원하는 구간의 누적합을 구할 수 있게 되었다.
그림으로 보면, 주황색 부분 = 45 - (초록색 +초록색) + 빨간색이 된다.
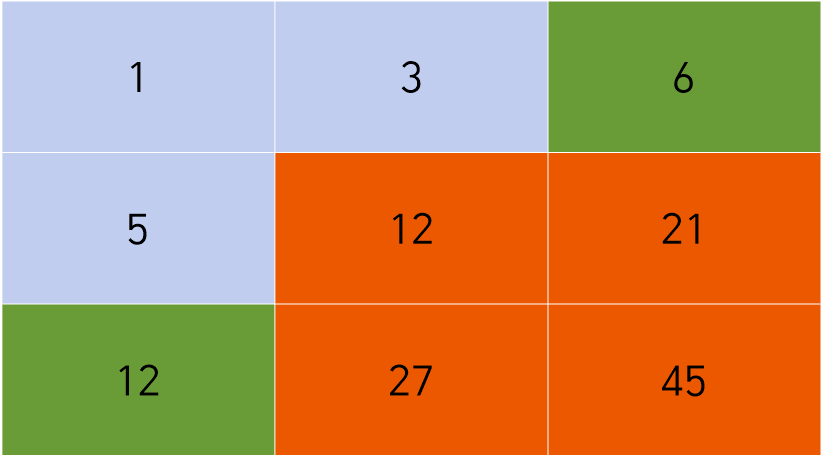

이걸 코드로 구현해보자.
구했던 값을 재활용한다는 점에서 DP(Dynamic) Programming이라고 할 수 있으며 , N^2만 해주면, 매번 O(N^2)할 필요없이, 누적합을 과정이 수식으로 나타난다는 점에서, O(N*N*M) => O(N*2 +M)로 개선이 되었다고 볼 수 있다.
# DP
import sys
input= sys.stdin.readline
N,M = map(int,input().split())
board=[list(map(int,input().split())) for _ in range(N)]
DP=[[0 for _ in range(N+1)] for _ in range(N+1)]
# 행 누적합
for i in range(1,N+1):
for j in range(1,N+1):
DP[i][j] = DP[i][j-1]+board[i-1][j-1]
# 열 누적합
for i in range(1,N+1):
for j in range(1,N+1):
DP[i][j] = DP[i-1][j] +DP[i][j]
for _ in range(M):
y1,x1,y2,x2=map(int,input().split())
ans=DP[y2][x2] - (DP[y2][x1-1] + DP[y1-1][x2]) + DP[y1-1][x1-1]
print(ans)'알고리즘 문제(SOL)' 카테고리의 다른 글
| [백준/1946/파이썬] 신입사원 (0) | 2022.03.10 |
|---|---|
| [백준/6588/파이썬] 골드바흐의 추측 (0) | 2022.03.10 |
| [백준/1992/파이썬] 쿼드 트리 (0) | 2022.03.08 |
| [백준/9020/파이썬] 골드바흐의 추측 (0) | 2022.03.08 |
| [백준/2444/파이썬] 별 찍기 7 (0) | 2022.03.07 |