개념
- MST(Minnimal Spanning Tree)를 알아내는 알고리즘 중 하나로, Graph를 탐사하는 방법 중 하나이기도 합니다.
- Graph를 탐사하는 과정을 보면, 모든 정점들을 가장 적은 비용으로 연결하기 위해서 사용되는 알고리즘입니다.
MST(Minimal Spanning Tree)
- Minimal Spanning Tree는 최소 신장 트리라고도 합니다.
- Spanning Tree가 뭔지 수학적 정의도 있고, 말로 정의하는 것도 좋지만, 그림으로써 먼저 이해하는게 좋습니다.
아래와 같은 그래프가 있다고 합시다.
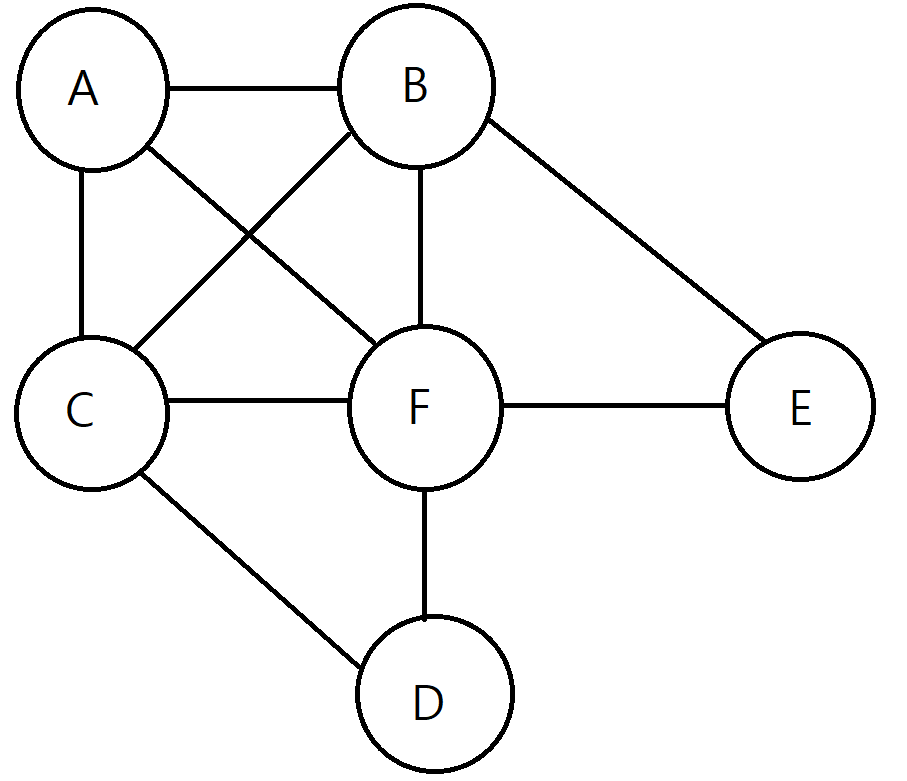
위 그래프의 Spanning Tree
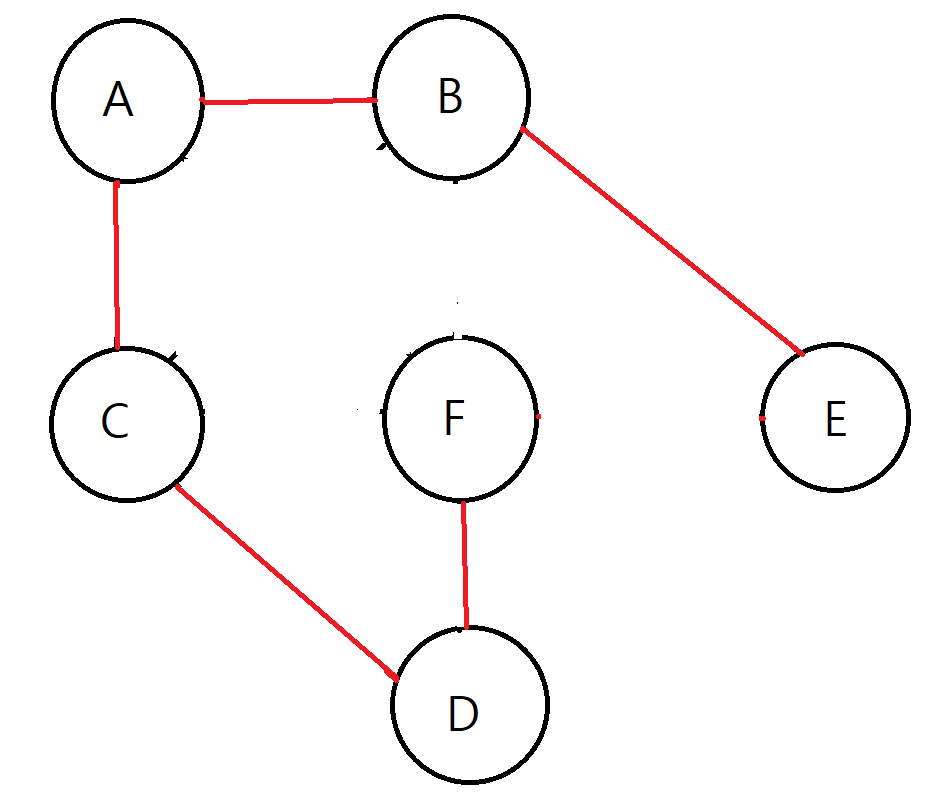
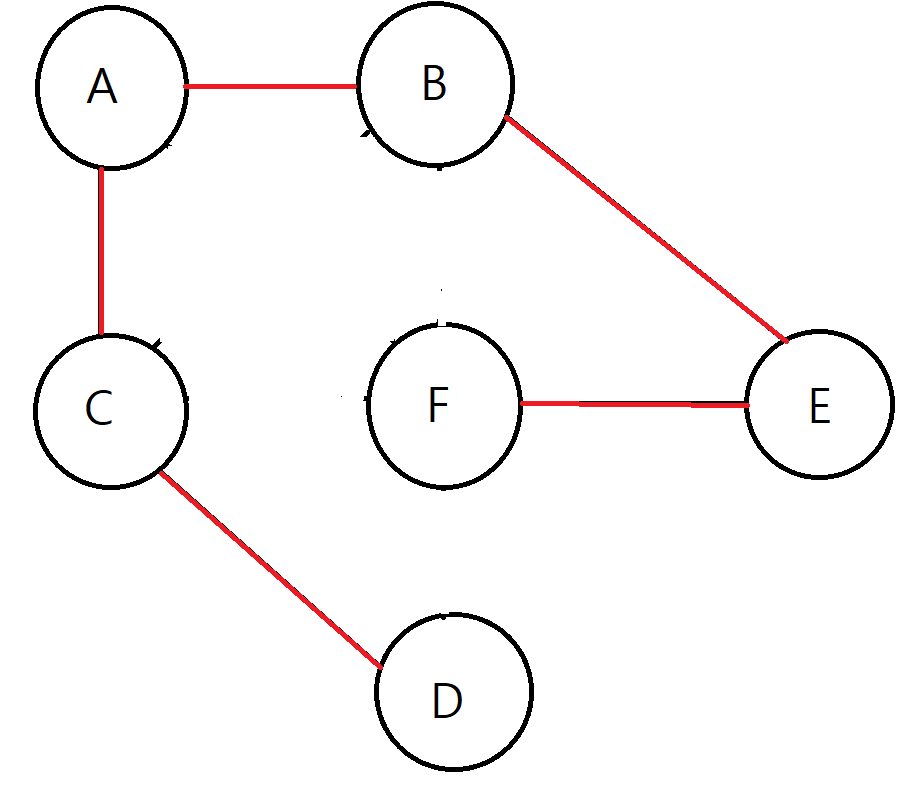

위의 그림들을 먼저 보고, 하나씩 특징들을 생각해봅시다.
Spanning Tree
- 모든 노드를 사이클 없이 방문하는 Tree
- Tree 이기 때문에, 모든 노드 -1개의 간선을 갖는다.
- 한 그래프내에는 여러가지 Spanning Tree가 존재한다.
- 이때, 각각의 간선들의 가중치의 합이 최소가 되는 Spanning Tree를 Minimal Spanning Tree, MST 라고 합니다.
크루스칼 알고리즘
크루스칼 선생님은 모든 노드들을 어떻게 최소의 비용으로 구한 과정을 봅시다.
1. 비용을 오름차순으로 정렬한다.(혹은, 작은 가중치를 가진 간선부터 연결한다)
2. 사이클이 생기면 안되므로, 매번 사이클 체크를 해주면서 노드에 간선을 하나씩 연결해준다. (Disjoint Set 사용)
3. 1,2 과정을 모든 노드가 연결될때 까지 반복해줍니다. 모든 노드가 연결되면 최초의 가중치 합이 우리가 구하는 최소비용이 됩니다.
크루스칼 알고리즘의 Flow-Chart
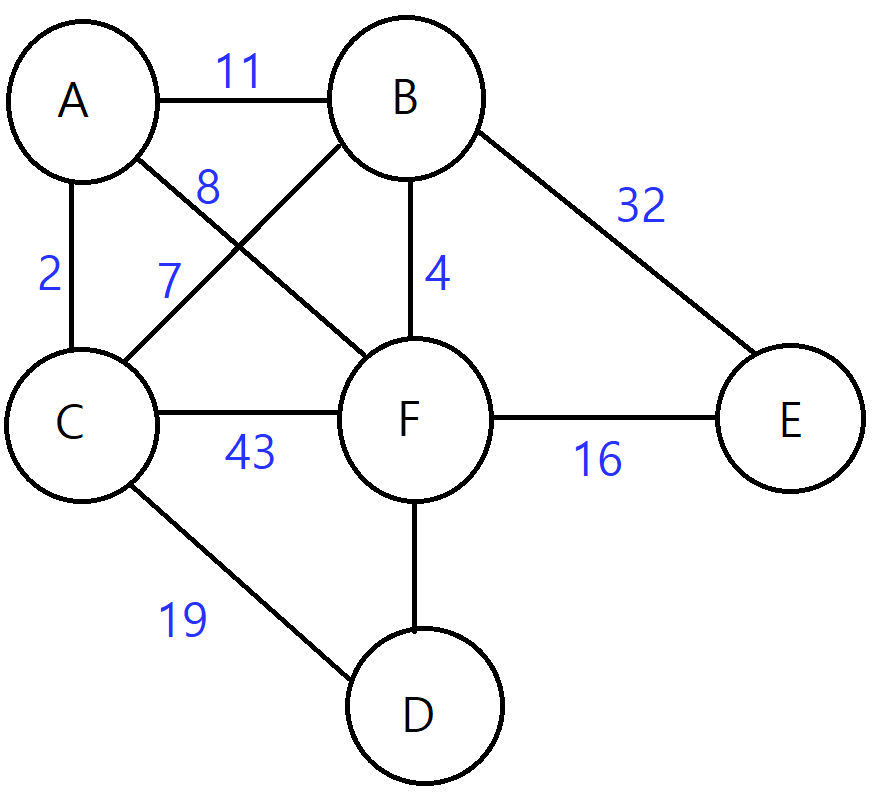

Flow 1
1. 가중치가 가장 작은 , 연결할 간선을 고른다.
2. A-C는 서로 다른 Parent를 갖고 있기 때문에, 사이클이 형성되지 않는다..
3. A-C를 같은 Parent를 갖게 해준다.(연결해준다)
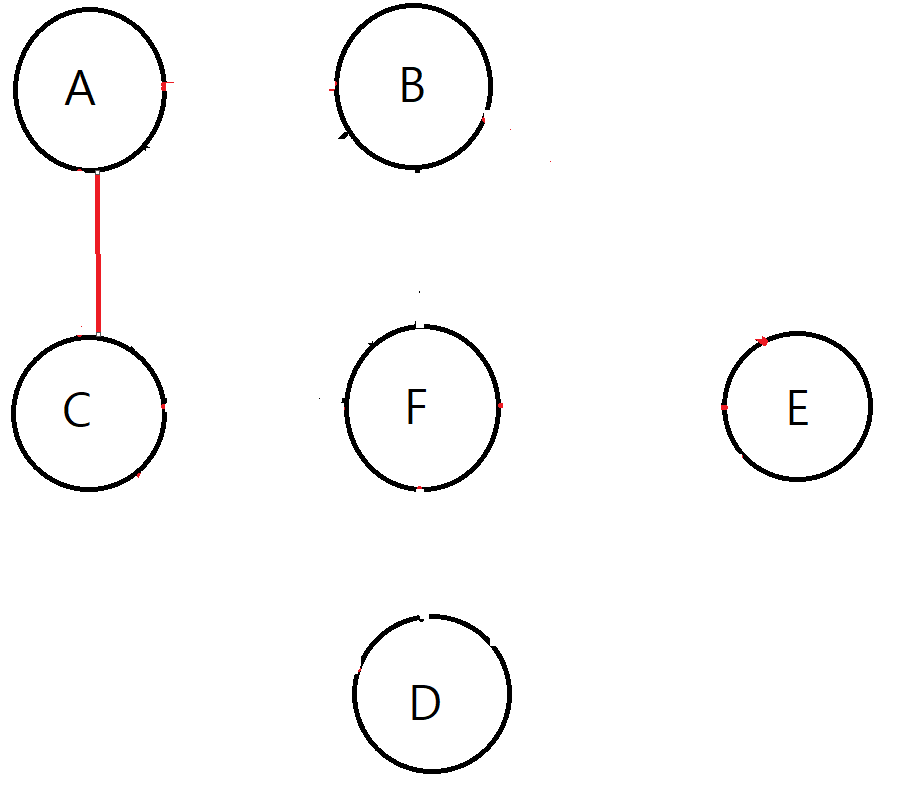

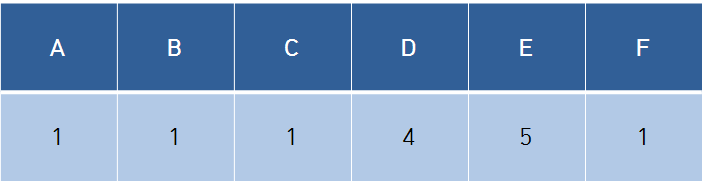
Flow 2
1. 가중치가 가장 작은 , 연결할 간선을 고른다.
2. B-F는 서로 다른 Parent를 갖고 있기 때문에, 사이클이 형성되지 않는다..
3. B-F를 같은 Parent를 갖게 해준다.(연결해준다)


Flow 3
1. 가중치가 가장 작은 , 연결할 간선을 고른다.
2. C-B는 서로 다른 Parent를 갖고 있기 때문에, 사이클이 형성되지 않는다..
3. C-B를 같은 Parent를 갖게 해준다.(연결해준다)

Flow4 , Flow 5
- A-F는 같은 부모 Parent를 갖고 있기 때문에, 사이클이 형성이 된다. A-F는 연결하지 않는다.
- A-B는 같은 부모 Parent를 갖고 있기 때문에, 사이클이 형성이 된다. A-B는 연결하지 않는다.
Flow 6
1. 가중치가 가장 작은 , 연결할 간선을 고른다.
2. F-E는 다른 부모 Parent를 갖고 있기 때문에, 사이클이 형성이 되지 않는다.
3. F-E를 연결한다.
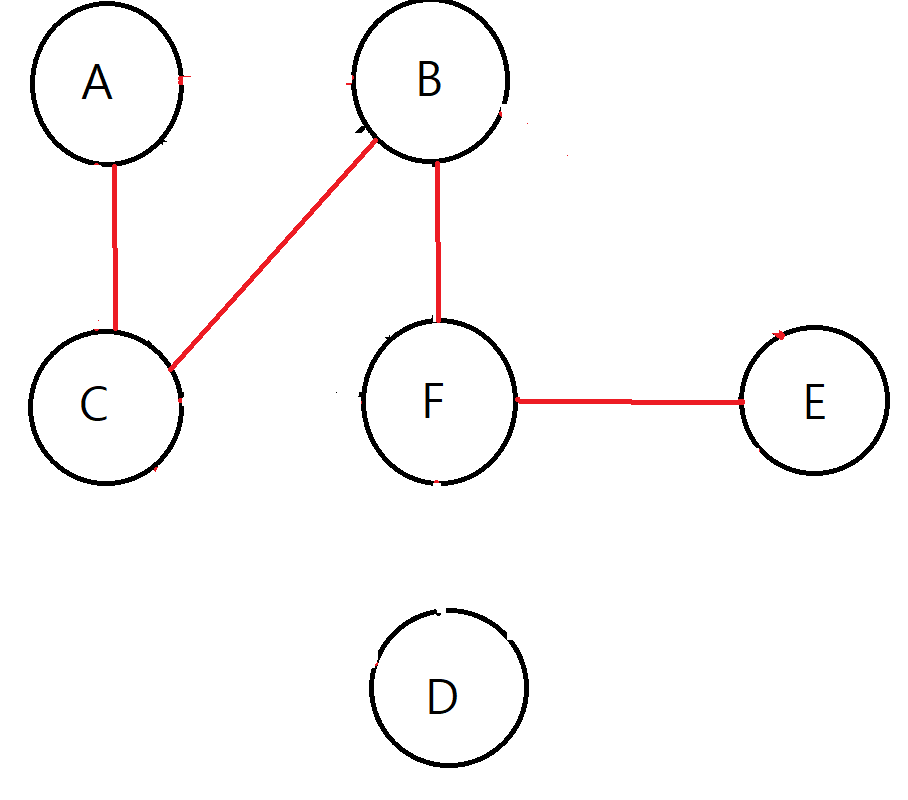
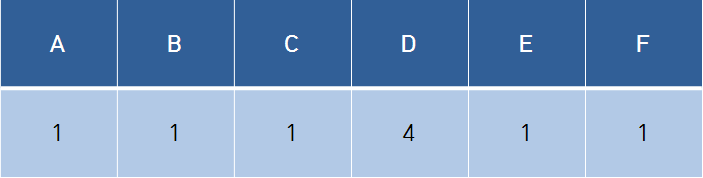
Flow 7
1. 가중치가 가장 작은 , 연결할 간선을 고른다.
2. C-D는 다른 부모 Parent를 갖고 있기 때문에, 사이클이 형성이 되지 않는다.
3. C-D를 연결한다.
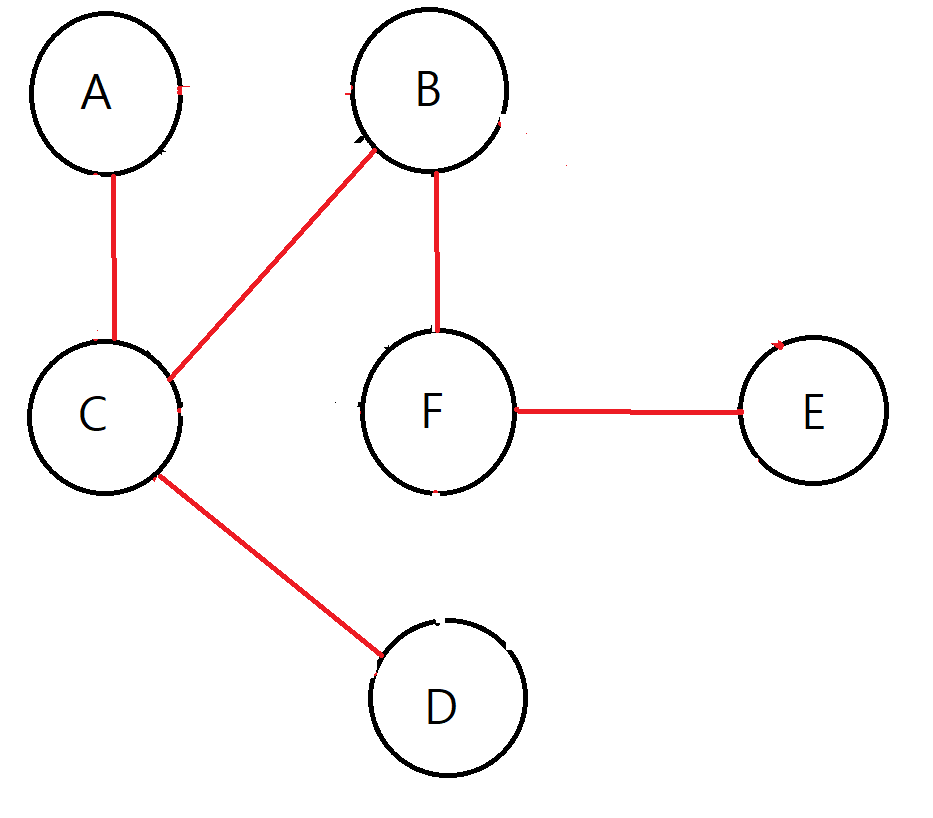

최소 가중치(mst_cost) : 2+7+4+16+19 = 48
코드
import sys
input= sys.stdin.readline
V,E=map(int,input().split())
graph=[]
parent=[x for x in range(V+1)]
def find(target):
if target ==parent[target]:
return target
parent[target] = find(parent[target])
return parent[target]
def union(a,b):
a=find(a)
b=find(b)
if a<b:
parent[b] =a
else:
parent[a] =b
# 그래프 추가
for i in range(E):
a,b,c=map(int,input().split())
graph.append((a,b,c))
graph.sort(key=lambda x:x[2])
tree_edge=0
mst_cost=0
# Kruskal의 핵심. V-1이 될 때까지 작은 것부터 차례대로, 합쳐본다.
while True:
if tree_edge==V-1:
break
u,v,cost=graph.pop(0)
if find(u) != find(v):
union(u,v)
mst_cost+=cost
tree_edge+=1
print(mst_cost)TEST CASE
'알고리즘 개념(Concept)' 카테고리의 다른 글
| [알고리즘/개념/그래프] 위상 정렬(Topological Sort) (0) | 2022.04.08 |
|---|---|
| [알고리즘/DP/개념] 팰린드롬 (0) | 2022.04.04 |
| [알고리즘/개념/그래프] Dijkstra 최단경로 알고리즘 (0) | 2022.03.18 |
| [알고리즘,개념] Binary search, Parametric Search (0) | 2022.02.10 |
| [개념/자료구조/파이썬] Disjoint Set, Union-Find 구조 (0) | 2022.02.02 |