Binary Search
"Searching"의 수많은 방법 중에 하나인 Binary Search에 대해서 알아보자!
이분 탐색은 백준에서 문제를 보면, 이게 이분 탐색인지 뭔지 잘 모를때가 많다. 그래서, 개념을 자신의 껄로 완벽하게 만들어야한다.
이분 탐색의 특징
- 자료가 정렬이 되어있는 상태여야 한다.
- 모든 탐색 범위를 전부 탐색하지 않는다. Target을 정하고, Target과 중간값의 대소관계에 따라서, 탐색 범위를 줄여간다.
- 선형 탐색보다 엄 ~ 청 빠른 성능을 자랑한다. (반씩 줄여나가기 때문에, O(logN))

개념은 정말 간단하다.
- IF) Target<mid : mid의 왼쪽 탐색
- IF) Target>mid : mid의 오른쪽 탐색
- IF) target==mid : 값 반환
하지만, 구현은 헷갈리기 쉬우니까, 정확하게 구현할줄 알아야한다.
- 탐색 범위를 설정해준다. (이 부분이 문제로 나오면 생각보다 까다롭다.)
- 탐색할 대상을 정해준다.
- 탐색할 대상과 , mid 값에 대한 대소관계에 따라서, 탐색 범위를 조정해준다.
list1=[1,2,3,4,6,9,10,15,51,211,2215]
def binary_search(list,searchnum):
lo=0
high=len(list1)-1
while lo<=high:
mid = (lo+high)//2
if searchnum>list1[mid]:
lo=mid+1
continue
if searchnum<list1[mid]:
high=mid-1
continue
if searchnum == list1[mid]:
return mid
return -1
print(binary_search(list1,200))
아래 문제를 풀면서 위 개념을 활용해보자.
https://www.acmicpc.net/problem/1920
1920번: 수 찾기
첫째 줄에 자연수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1 ≤ M ≤ 100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들
www.acmicpc.net
Parametric Search
사실, 이분탐색의 개념은 "탐색"의 개념이 짙게 깔려있지만, 우리의 컴공인들은 이 이분탐색의 개념을 좀 더 확장해서, Optimal(최적화) 문제에 활용하기 시작했다. 그게 바로 Parametric Search라는 방법이다.
이 개념은 예시를 들면 더 깔끔하게 이해되기에, 예시를 적절하게 들어보겠습니다.
사람들은 나이순으로 정렬되어있고, 나이가 14살 이상은 마인크래프트를 싫어한다고 합니다.
우리는 여기서 "마인크래프트를 좋아하는 나이가 가장 많은 친구는 누구일까요?" 라는 질문에 대답을 한다고 하자.
직관적으로 떠올리기 쉬운 방법은 앞에 친구부터 순서대로 마인크래프트 좋아하니?라고 물어서 처음으로 "아니요!" 대답이 나온 바로 앞의 친구가 가장 나이가 많은 마인크래프트를 좋아하는 친구일겁니다.

하지만, 우리 컴공이들은, 이분탐색이라는 개념을 알기 때문에, 순차적으로 묻기보다는 중간 사람한테 딱 물어봅니다.
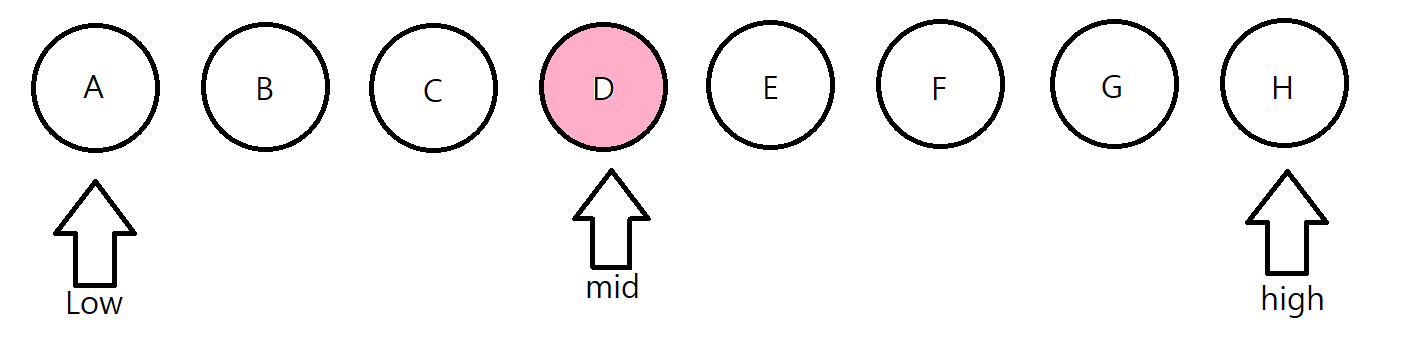
"D야, 너 마인크래프트 좋아해?" 대답은 NO!(14세 이상인 경우), Yes(14세 미만인 경우)라고 합니다.
D는 다행히도, 마인크래프트를 좋아한다고 합니다.
그럼, 우리는 D의 다음 친구부터만 보면 됩니다. (Low = mid +1)
G한테 이번에 물어봅니다. 너 마인크래프트 좋아해 ? 대답은 NO 입니다.
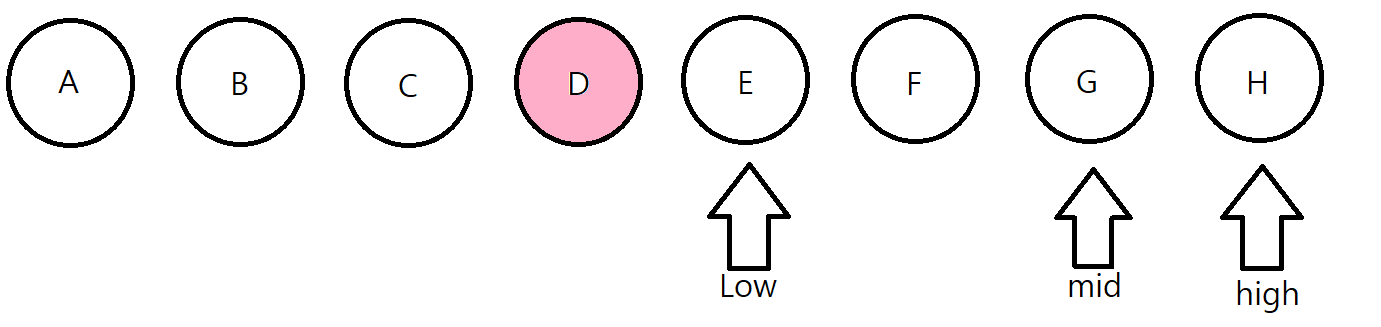
이번에는 F한테 물어봅니다.
F야 너 마인크래프트 좋아해? 대답은 YES 입니다. 그렇다면, 우리는 알 수 있습니다. "F"가 마인크래프를 좋아하는 사람들 중에서는, 제일 나이가 많은 친구라는걸 알 수 있습니다!
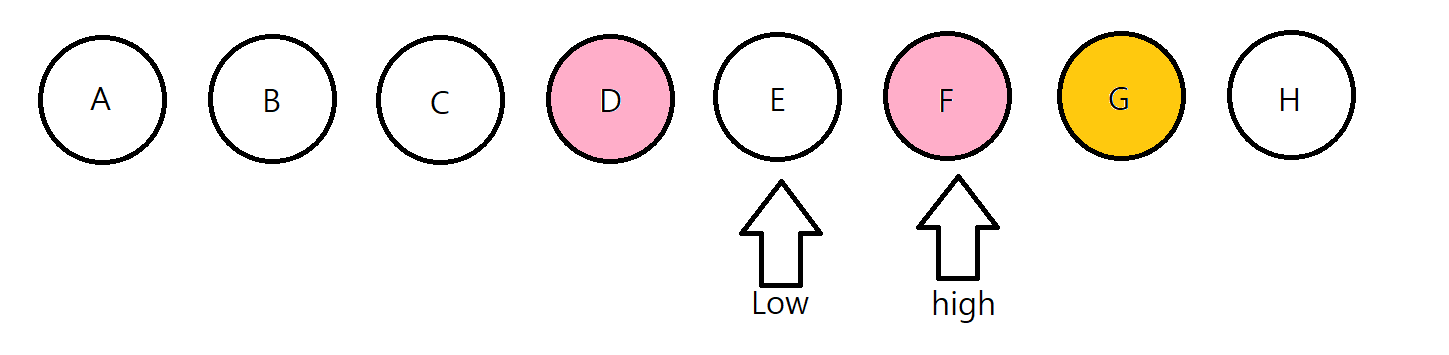
E한테는 물어볼 필요가 없습니다. 왜냐하면, 나이순으로 정렬이 되어있는데, F가 마인크래프트를 좋아한다고 말한 순간, F의 나이가 제일 많은건 자명한 사실이 됩니다.
이처럼, 어떤 최적화가 필요한 문제를 , 특정 조건의 Scope를 정해서, 그 중의 최솟/최댓값(경계값)을 찾는 문제로 바꾸는 방법을 parametric search라고 합니다.
우리는 선형적으로 묻는다면, 5번만에 찾았겠지만, 우리는 3번만에 찾았습니다. 이게 N이 커지면 커질수록 격차는 더 벌어질겁니다. 이 과정에서 이분탐색의 탐색하는 방법이 응용되었을 뿐입니다.
따라서, 어떤 특정 경계값을 찾을 때는 파라메트릭 서치 -> 구현은 이분탐색과 비슷하게 구현이 됩니다.
'알고리즘 개념(Concept)' 카테고리의 다른 글
| [알고리즘/개념/그래프] 크루스칼 알고리즘(KrusKal Algorithm) (0) | 2022.04.01 |
|---|---|
| [알고리즘/개념/그래프] Dijkstra 최단경로 알고리즘 (0) | 2022.03.18 |
| [개념/자료구조/파이썬] Disjoint Set, Union-Find 구조 (0) | 2022.02.02 |
| [알고리즘,개념] 연쇄 행렬 곱셈 문제(CMM) (0) | 2022.01.17 |
| [알고리즘,개념,DP] LIS (Longest Increasing Subsequence) (0) | 2022.01.13 |